报告题目：Global boundedness and large time behavior in ahigher-dimensional quasilinear chemotaxis system withconsumption of chemoattractant

报告人：穆春来教授(重庆大学)

报告时间：2024年4月21日上午09点20 分-10点20分

报告地点：数理楼135

报告摘要：Thistalkdeals with the following quasilinear chemotaxis system with consumption of chemoattractant

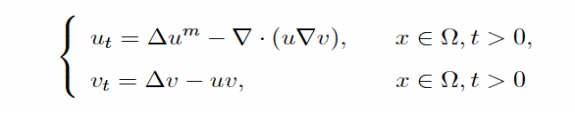
in a bounded domain $\Omega\subseteq \R^3 (N\geq 3)$ with smooth boundary $\partial\Omega$. It is shown that if $m>\max\{1,\frac{3N-2}{2N+2}\}$, for any reasonably smooth nonnegative initial data, the corresponding no-flux type initial-boundary value problem possesses a globally bounded weak solution. Furthermore, the solution converges to the spatially homogeneous equilibrium $(\bar{u}_0, 0)$ in an appropriate sense as $t\rightarrow 0$, where $\bar{u}_0=\frac{1}{|\Omega|}\int_\Omega u_0$. In particular, the result extends the previous global boundedness result for $m>\frac{3N-2}{3N}$, and improves the global existence result for $m>\frac{3N}{3N+2}$.

报告人简介：穆春来，教授，现任重庆大学必赢473官方网站院长，博士生导师，中国数学会理事，重庆市数学会副理事长，主要从事非线性偏微分方程、生物数学和图像处理理论和应用研究。2005年入选“教育部新世纪优秀人才”计划，2008入选重庆市学术与技术带头人。先后承担了多项国家自然科学基金、教育部新世纪优秀人才基金、教育部优秀年轻教师基金、重庆市自然科学重点基金等科研项目20余项。2015年获得重庆市自然科学奖二等奖一项；2014年获得国家教学成果二等奖一项；2019年获得教育部自然科学奖二等奖。已在MMMAS、JDE、JNS、Proc. Roy. Soc. EdinghSec. A、DCDS等国内外重要数学期刊发表论文250余篇。